核技巧和非线性 SVM

在原始 SVM 只支持线性样本的基础上，引入核技巧 (Kernel Trick) 可以对非线性的样本进行分类。算法思想为将输入向量映射到高维空间，然后用超平面划分。本文中有举例说明。

核技巧原理

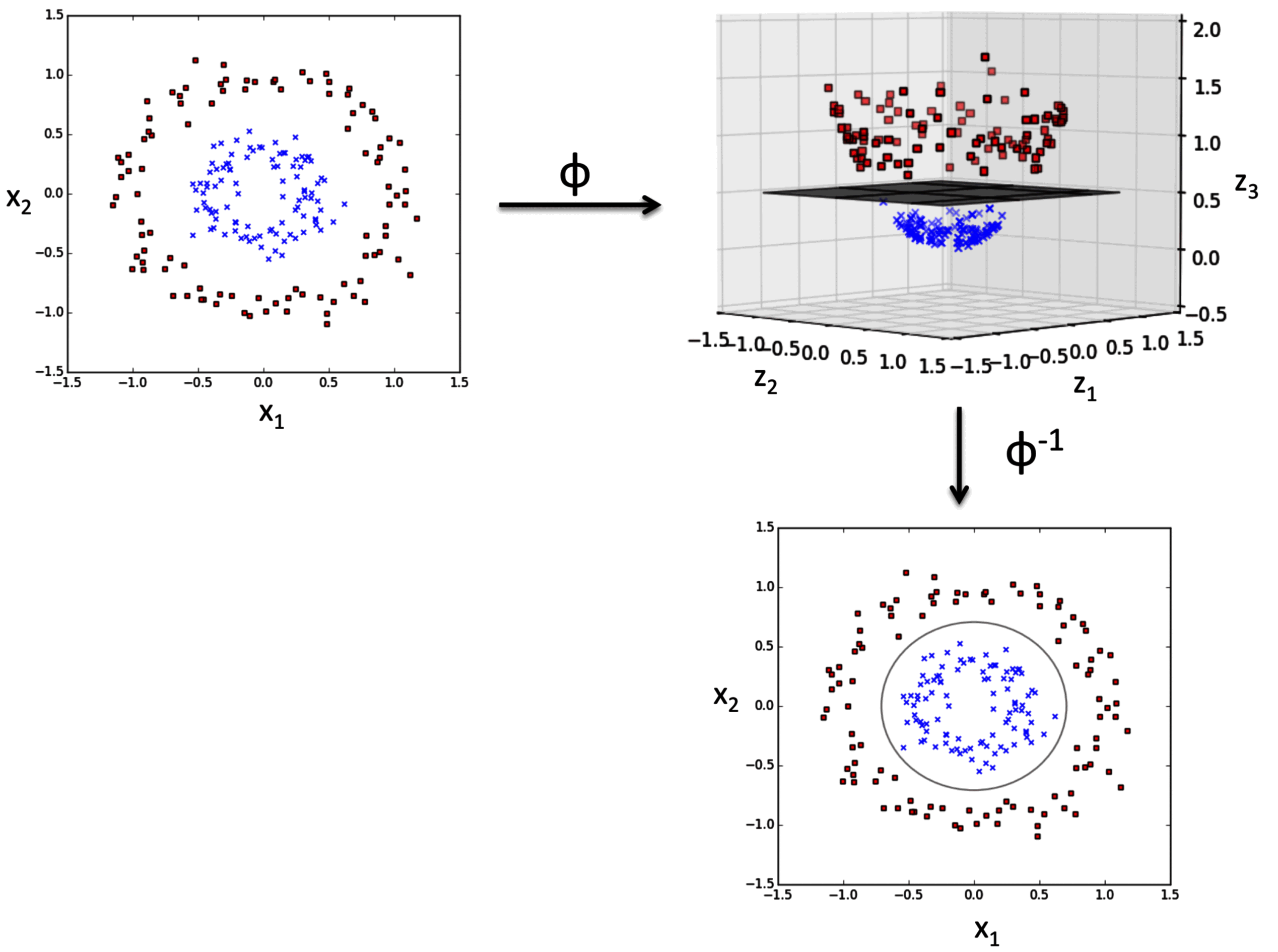
下图描述了 SVM 如何将低维非线性可分的问题转换为高维度线性可分。

如图所示，原始的内环 (红色样本) 和外环 (蓝色样本) 不能线性分割。

通过非线性变换 $\phi (x)$ ，将原始二维数据集映射到新的三维特征空间，如右上子图。

\begin{align} \phi (x_1, x_2) = (z_1, z_2, z_3) = (x_1, x_2, x_1^2 + x_2^2) \end{align}

将分离样本的线性超平面 $z_3 = c$ 其投影回原始特征空间，则得到原始二维空间的非线性决策边界 $x_1^2 + x_2^2 = c$ 。

数学表达

核技巧的数学描述如下：

\begin{align} k(\boldsymbol x^{(i)}, \boldsymbol x^{(j)}) = \phi(\boldsymbol x^{(i)})^T \phi(\boldsymbol x^{(j)}) \end{align}

以常见的 (高斯) 径向基函数 (Radial Basis Function，RBF) 为例，核函数为：

\begin{align} k(\boldsymbol x^{(i)}, \boldsymbol x^{(j)}) = \exp \left(- \cfrac {||\boldsymbol x^{(i)} - \boldsymbol x^{(j)}||^2} {2\sigma^2} \right) \end{align}

上式通常简化为：

\begin{align} k(\boldsymbol x^{(i)}, \boldsymbol x^{(j)}) = \exp \left(- \gamma {||\boldsymbol x^{(i)} - \boldsymbol x^{(j)}||^2} \right) \end{align}

其中 $\gamma = \cfrac 1 {2\sigma^2}$ 为需要优化的超参数。

非线性 SVM 实现

以 Iris 数据集为例，基于 Scikit-learn 的实现如下 (其中决策边界绘制函数 plot_decision_regions 请参见之前的文章)：

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler

iris = datasets.load_iris()
X = iris.data[:, [2, 3]]
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=1, stratify=y
)

sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
X_combined_std = np.vstack((X_train_std, X_test_std))
y_combined = np.hstack((y_train, y_test))

svm = SVC(kernel="rbf", random_state=1, gamma=0.2, C=1.0)
svm.fit(X_train_std, y_train)

plot_decision_regions(
    X_combined_std, y_combined, classifier=svm, test_idx=range(105, 150)
)
plt.xlabel("petal length [standardized]")
plt.ylabel("petal width [standardized]")
plt.legend(loc="upper left")
plt.show()

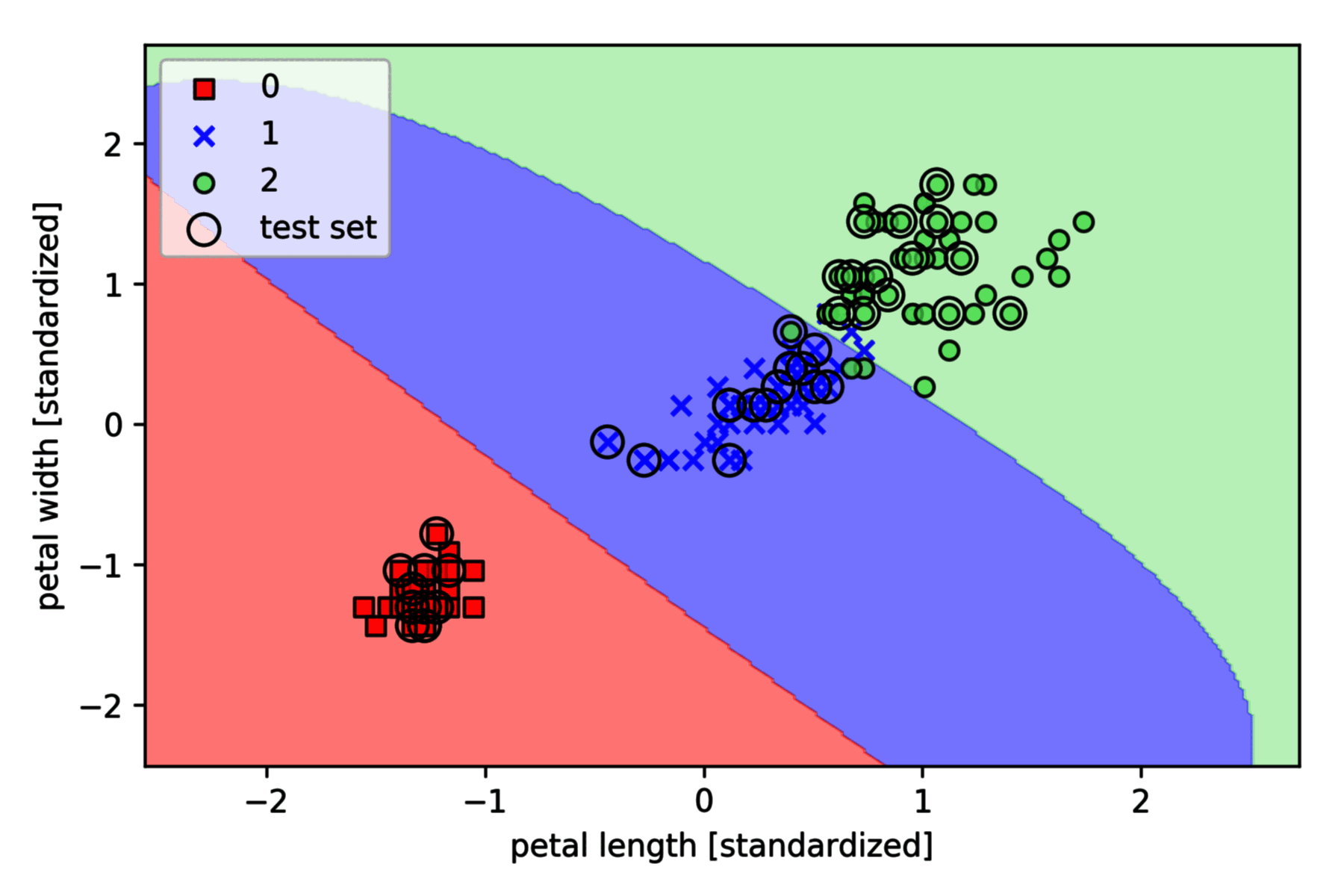
上图的决策边界是较为合理的曲线。

将 SVC 的超参数 $\gamma$ 增大至 $100$ ，观察决策边界的变化：

svm = SVC(kernel="rbf", random_state=1, gamma=100.0, C=1.0)

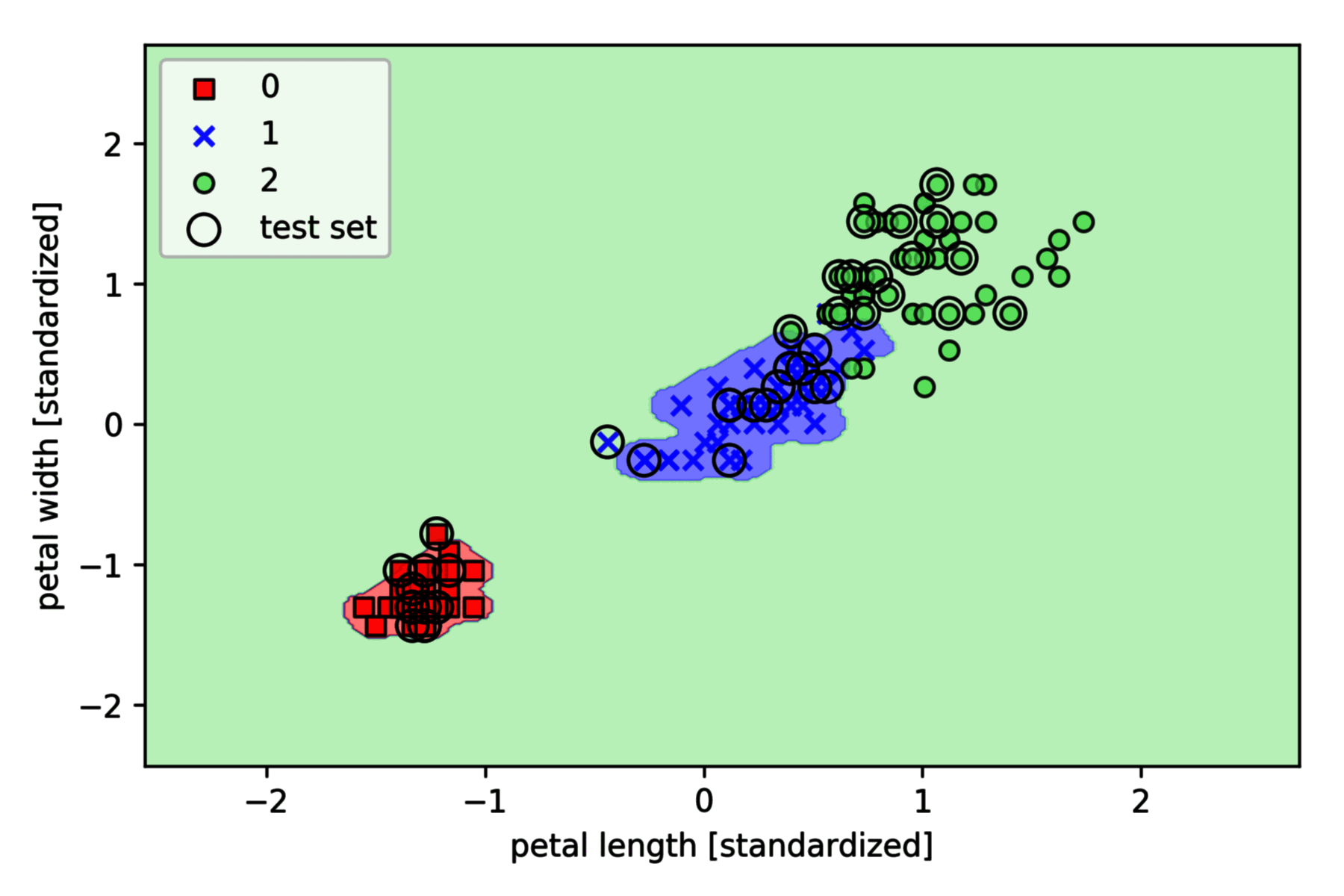
可以看到，类 1 和类 2 的边界非常紧凑，样本空间远远小于类 3 的样本空间。

当 $\gamma$ 较大时，容易出现过拟合情况，在实际应用中需要控制 $\gamma$ 的大小在合理范围。

核技巧原理​

数学表达​

非线性 SVM 实现​

核技巧原理

数学表达

非线性 SVM 实现