跳到主要内容

线性 SVM

支持向量机 (Support Vector Machine，SVM) 是一种监督式学习方法，其学习策略为最大化样本与超平面 (即决策边界) 之间的间隔。本文介绍线性 SVM 的原理及实现。

间隔被定义为分离超平面与最靠近这个超平面的训练样本之间的距离。

这些影响边界的特殊样本称为支持向量，也是算法称为支持向量机的原因。

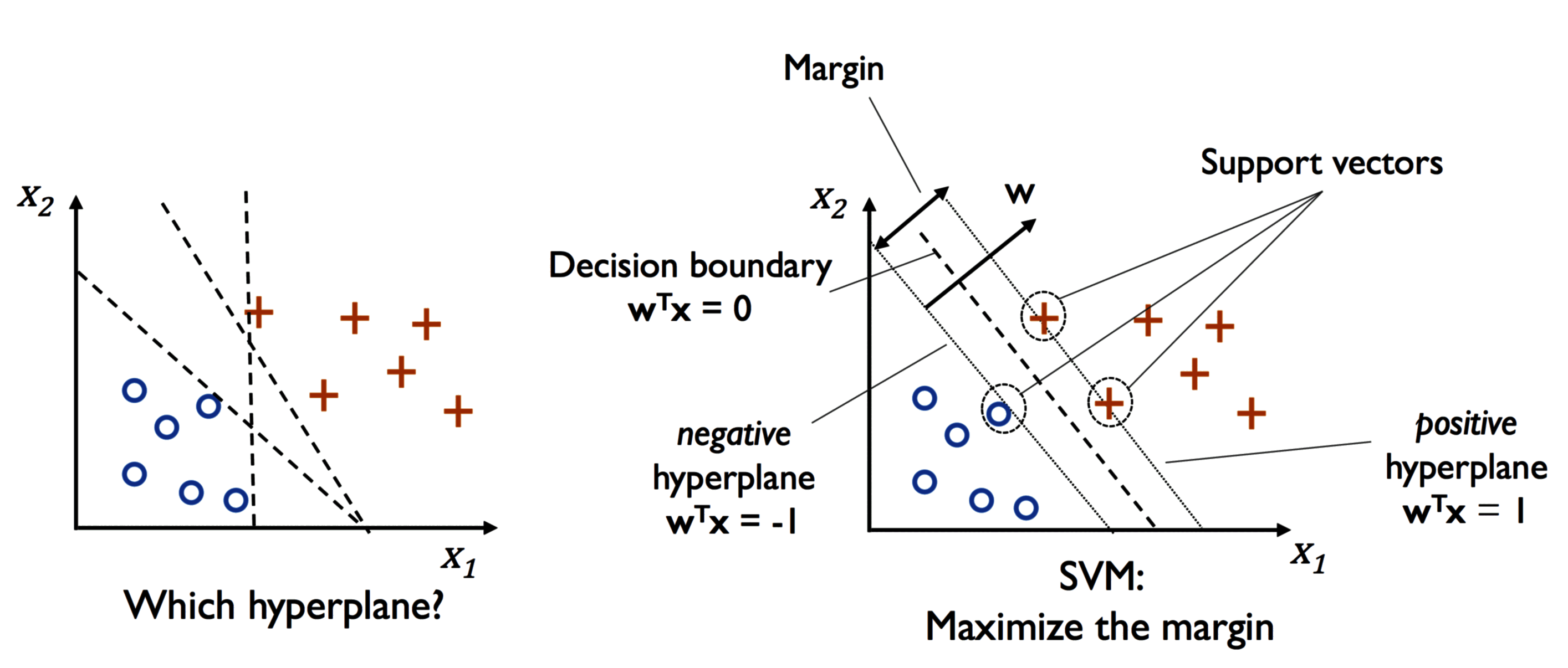
硬间隔 SVM​

为了得到边缘最大化，与决策边界平行的正负超平面可以用数学表示如下：

w0+wTxpos=1w0+wTxneg=−1\begin{align} w_0 + {\boldsymbol w^T} {\boldsymbol {x_{pos}}} & = 1 \\ w_0 + {\boldsymbol w^T} {\boldsymbol {x_{neg}}} & = -1 \end{align}

相减得到：

wT(xpos−xneg)=2\begin{align} {\boldsymbol w^T} (\boldsymbol {x_{pos}} - \boldsymbol {x_{neg}}) = 2 \end{align}

对上式中的 wT\boldsymbol w^T 进行向量归一化：

wT∣∣w∣∣(xpos−xneg)=2∣∣w∣∣,where ∣∣w∣∣=∑j=1m(wj)2\begin{align} \frac {\boldsymbol w^T} {||\boldsymbol w||} (\boldsymbol {x_{pos}} - \boldsymbol {x_{neg}}) = \frac 2 {||\boldsymbol w||}, \quad where \ ||\boldsymbol w|| = \sum_{j=1}^m (w_j)^2 \end{align}

这两个超平面之间的距离是 2∣∣w∣∣\cfrac 2 {||\boldsymbol w||}，要使两平面间的距离最大，我们需要最小化 ∣∣w∣∣||\boldsymbol w||。

同时为了使得样本数据点都在超平面的间隔区以外，我们需要保证对于所有的 ii 满足以下条件之一：

w0+wTx(i)≥1,if y(i)=1w0+wTx(i)≤−1,if y(i)=−1\begin{align} w_0 + {\boldsymbol w^T} {\boldsymbol x^{(i)}} & \ge 1, \quad if \ y^{(i)} = 1 \\ w_0 + {\boldsymbol w^T} {\boldsymbol x^{(i)}} & \le -1, \quad if \ y^{(i)} = -1 \end{align}

上式等同于：

y(i)(w0+wTx(i))≥1,∀i\begin{align} y^{(i)}(w_0 + {\boldsymbol w^T} {\boldsymbol x^{(i)}}) \ge 1, \quad \forall i \end{align}

硬间隔 SVM 的目标是在上式约束条件下，最小化 ∣∣w∣∣||\boldsymbol w||；在实际中，一般是最小化 12∣∣w∣∣2\cfrac 1 2 ||\boldsymbol w||^2。

软间隔 SVM​

SVM 在软间隔分类器中引入了松弛变量 ξ\xi，它允许分类器对一些样本犯错，允许一些样本不满足硬间隔约束条件。

这样做可以避免 SVM 分类器过拟合，于是也就避免了模型过于复杂，降低了模型对噪声点的敏感性，提升了模型的泛化性能。

带松弛变量的分类器约束条件如下：

w0+wTx(i)≥1−ξ(i),if y(i)=1w0+wTx(i)≤−1+ξ(i),if y(i)=−1\begin{align} w_0 + {\boldsymbol w^T} {\boldsymbol x^{(i)}} & \ge 1 - \xi ^{(i)}, \quad if \ y^{(i)} = 1 \\ w_0 + {\boldsymbol w^T} {\boldsymbol x^{(i)}} & \le -1 + \xi ^{(i)}, \quad if \ y^{(i)} = -1 \end{align}

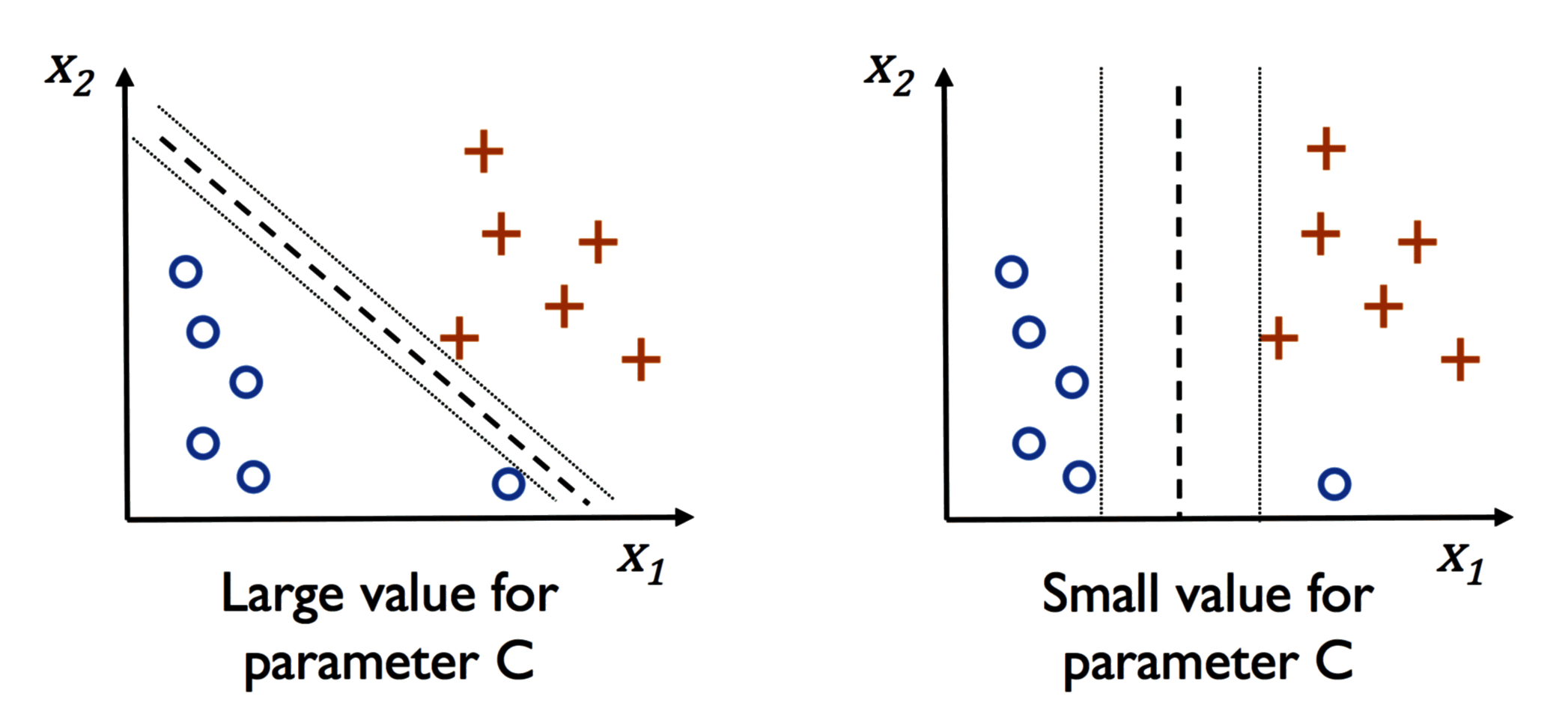
软间隔 SVM 的目标是最小化 12∣∣w∣∣2+C(∑iξ(i))\cfrac 1 2 ||\boldsymbol w||^2 + C (\sum_i \xi ^{(i)})。

参数 CC 可以平衡偏差和方差。CC 越大，算法分类越严格，方差越高，过大的 CC 可能会引起过拟合；反之同理。

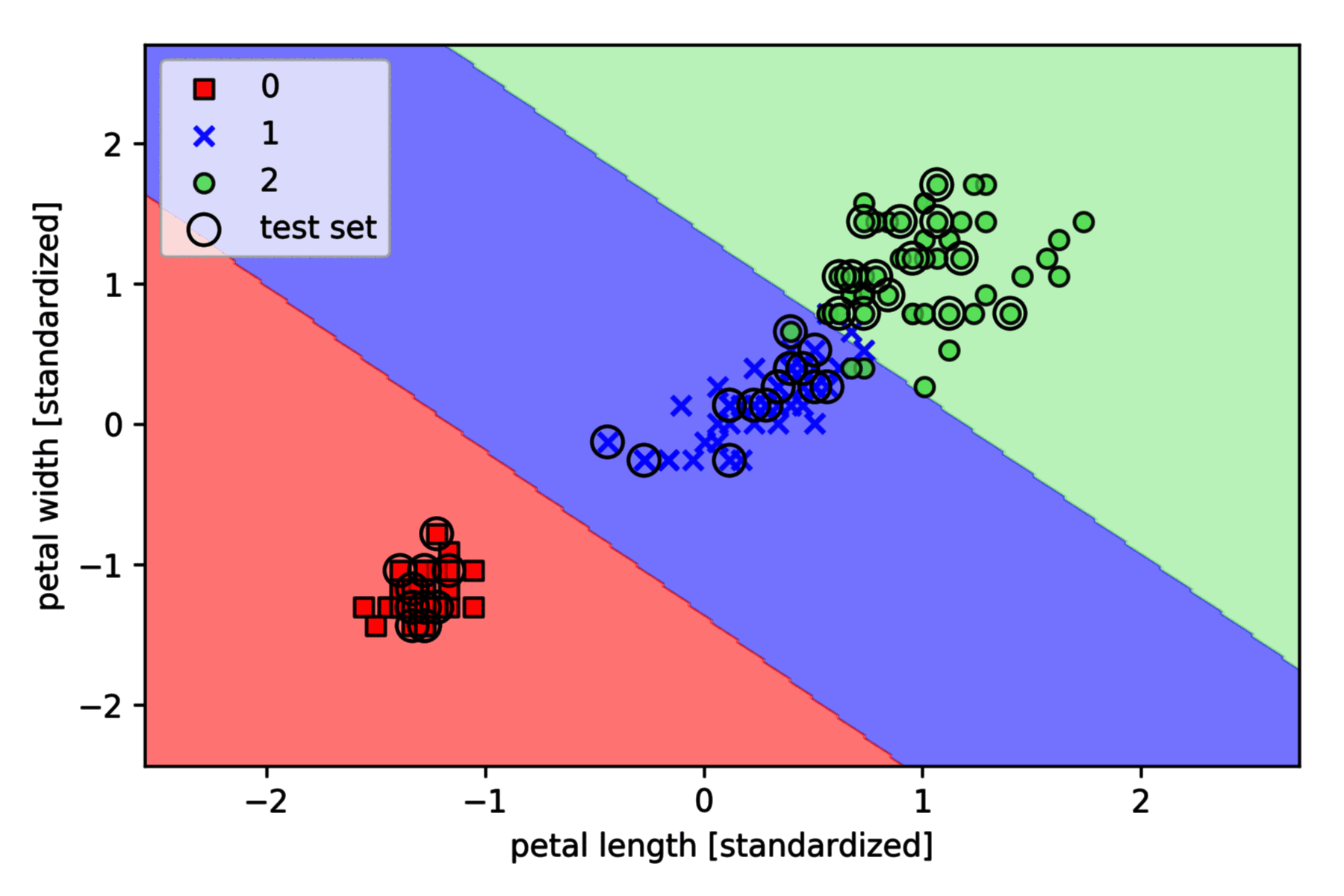
以 Iris 数据集为例，基于 Scikit-learn 的实现如下 (其中决策边界绘制函数 plot_decision_regions 请参见之前的文章)：

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler

iris = datasets.load_iris()
X = iris.data[:, [2, 3]]
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=1, stratify=y
)

sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
X_combined_std = np.vstack((X_train_std, X_test_std))
y_combined = np.hstack((y_train, y_test))

svm = SVC(kernel="linear", C=1.0, random_state=1)
svm.fit(X_train_std, y_train)

plot_decision_regions(
    X_combined_std, y_combined, classifier=svm, test_idx=range(105, 150)
)
plt.xlabel("petal length [standardized]")
plt.ylabel("petal width [standardized]")
plt.legend(loc="upper left")
plt.show()