ROC 和 AUC

在信号检测理论中，接收者操作特征 (Receiver Operating Characteristic，ROC) 曲线是是一种坐标图式的分析工具，通过计算 ROC 的曲线下面积 (Area Under Curve，AUC) 可以对分类模型进行评估。ROC 分析的是二分分类模型。

ROC 曲线通过绘制采用不同分类阈值时的 TPR (True Positive Rate) 与 FPR (False Positive Rate) 来选择模型。它展示了在不同分类阈值下，模型的性能表现。ROC 曲线的对角线可以被解释为随机猜测 (如丢硬币、正反面出现概率预测均是 50%)，并且落在对角线上方的分类模型优于随机猜测，落在对角线下方的分类模型比随机猜测更差。

AUC 是 ROC 曲线下的面积，即 ROC 曲线和横轴之间的面积。AUC 值的范围在 0 到 1 之间，其中 0.5 表示模型的预测性能等于随机猜测，而 1 表示完美分类器。AUC 值越接近 1，表示模型的性能越好。

下文将实现分类器的 ROC 曲线绘制，该分类器仅使用 wdbc 数据集中的两个特征来预测肿瘤是良性还是恶性。

数据导入和预处理

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import StratifiedKFold
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline

df = pd.read_csv(
    "https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/wdbc.data",
    header=None,
)
X = df.loc[:, 2:].values
y = df.loc[:, 1].values
le = LabelEncoder()
y = le.fit_transform(y)
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.20, stratify=y, random_state=1
)

ROC 曲线的 scikit-learn 实现

使用逻辑回归 pipeline，并采用折叠数为 3 的 StratifiedKFold，如下代码：

from sklearn.metrics import roc_curve, auc
from scipy import interp

pipe_lr = make_pipeline(
    StandardScaler(),
    PCA(n_components=2),
    LogisticRegression(penalty="l2", random_state=1, C=100.0),
)

X_train2 = X_train[:, [4, 14]]
cv = list(StratifiedKFold(n_splits=3, random_state=1).split(X_train, y_train))

fig = plt.figure(figsize=(7, 5))

mean_tpr = 0.0
mean_fpr = np.linspace(0, 1, 100)
all_tpr = []

for i, (train, test) in enumerate(cv):
    probas = pipe_lr.fit(X_train2[train], y_train[train]).predict_proba(X_train2[test])
    fpr, tpr, thresholds = roc_curve(y_train[test], probas[:, 1], pos_label=1)
    mean_tpr += interp(mean_fpr, fpr, tpr)
    mean_tpr[0] = 0.0
    roc_auc = auc(fpr, tpr)
    plt.plot(fpr, tpr, label="ROC fold {} (area = {:.2f}".format(i + 1, roc_auc))

plt.plot([0, 1], [0, 1], linestyle="--", color=(0.6, 0.6, 0.6), label="random guessing")

mean_tpr /= len(cv)
mean_tpr[-1] = 1.0
mean_auc = auc(mean_fpr, mean_tpr)
plt.plot(
    mean_fpr, mean_tpr, "k--", label="mean ROC (area = {:.2f}".format(mean_auc), lw=2
)

上面的代码通过从 SciPy 导入的 interp 函数插入了三次折叠的平均 ROC 曲线，并通过 auc 函数计算曲线下面积。

三次绘制的 ROC 曲线表明不同折叠之间存在一定程度的变化，并且 ROC AUC 的平均值 (0.76) 落在完美预测 (1.0) 和随机猜测 (0.5) 之间：

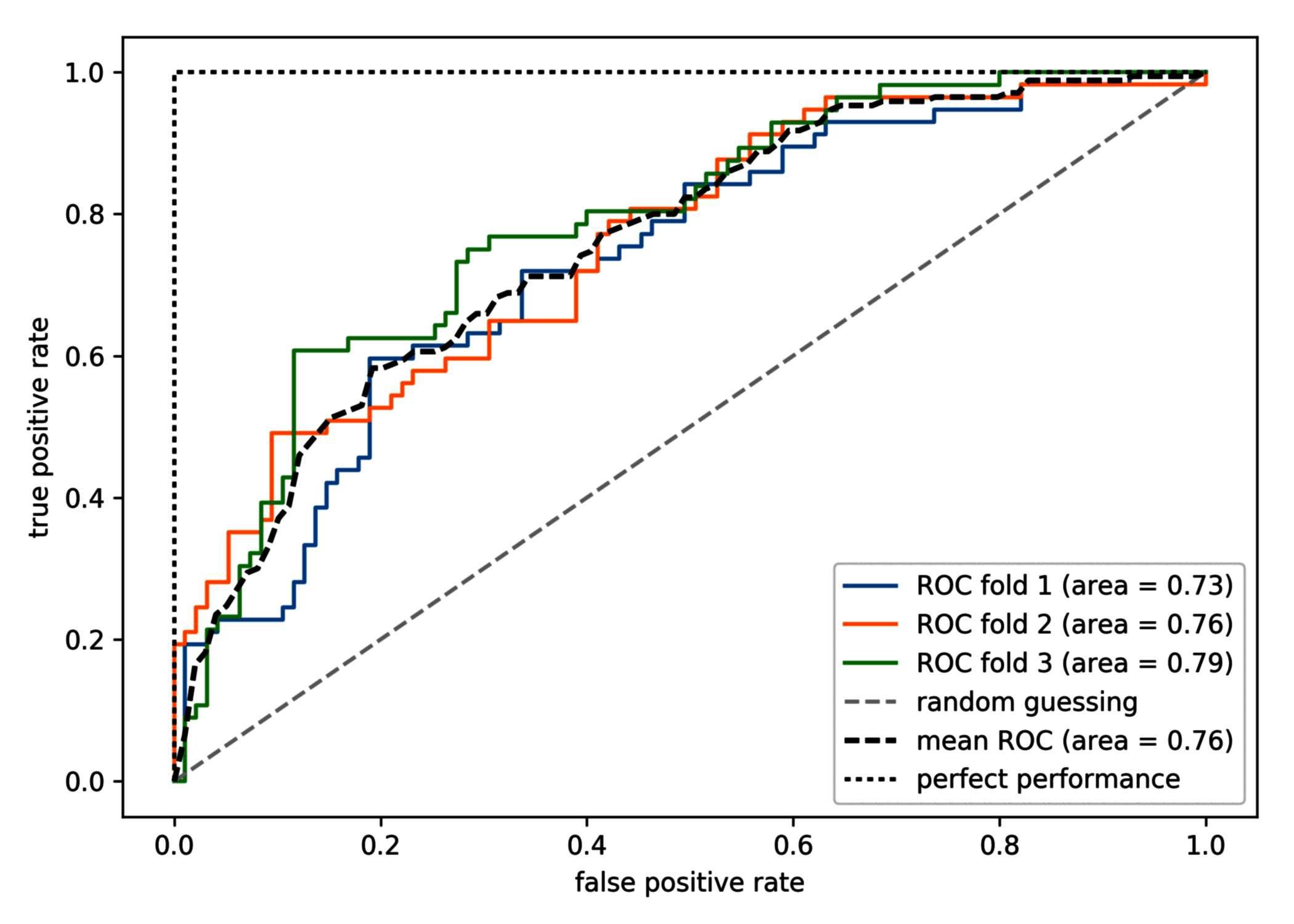
如果只需要用到 ROC AUC 分数，也可以直接导入 sklearn.metrics.roc_auc_score 函数。ROC AUC 分数可以对样本数量不平均的二分分类模型进行评估。

数据导入和预处理​

ROC 曲线的 scikit-learn 实现​

数据导入和预处理

ROC 曲线的 scikit-learn 实现