特征缩放

特征缩放 (Feature Scaling) 是将不同特征的值量化到同一区间的方法，也是预处理中容易忽视的关键步骤之一。除了极少数算法 (如决策树和随机森林) 之外，大部分机器学习和优化算法采用特征缩放后会表现更优。

特征缩放方法可分为包含归一化 (Normalization) 和标准化 (Standardization)。不同领域对这两个术语的定义可能不同，本文只对常用的定义进行介绍。

归一化

一般来说，归一化是指将特征重新缩放到 $[0，1]$ 的范围，属于极值缩放 (Min-Max Scaling) 的一种情况。其数学表达如下：

$$\begin{align} x_{norm}^{(i)} = \cfrac {x^{(i)} - x_{min}} {x_{max} - x_{min}} \end{align}$$

其中，$x^{(i)}$ 和 $x_{norm}^{(i)}$ 分别表示第 $i$ 个样本归一化前后的特征值，$x_{max}$ 和 $x_{min}$ 分别表示该特征的最大值和最小值。

在 scikit-learn 中，可通过 sklearn.preprocessing.MinMaxScaler 实现：

>>> from sklearn.preprocessing import MinMaxScaler
>>> mms = MinMaxScaler()
>>> X_train_norm = mms.fit_transform(X_train)
>>> X_test_norm = mms.transform(X_test)

标准化

标准化是将对特征缩放为服从正态分布，即平均值为 0、方差为 1。与归一化相比，标准化更适用于大部分学习算法。

以梯度下降法为例，如下左子图 (标准化前的收敛) 和右子图 (标准化后的收敛)：

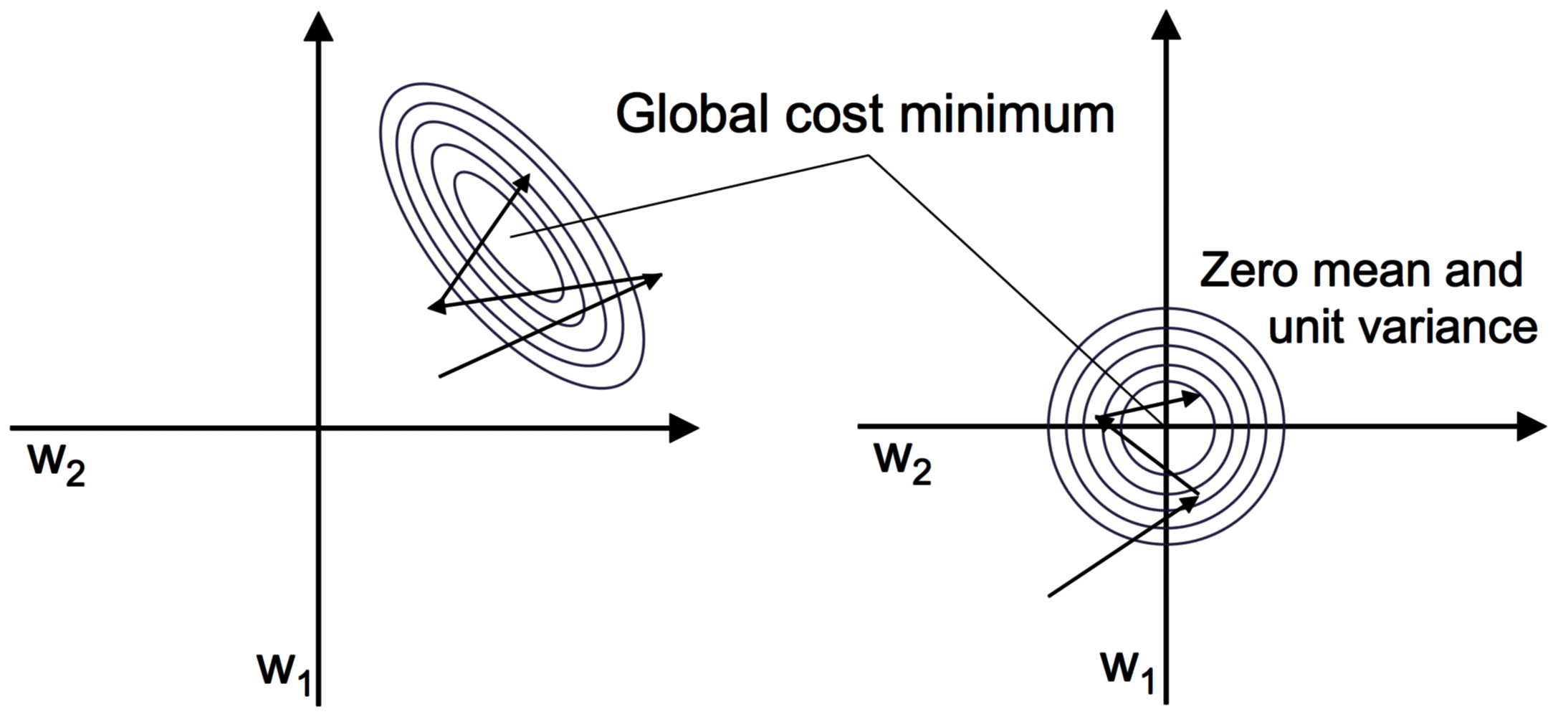
其数学表达如下：

$$\begin{align} x_{std}^{(i)} = \cfrac {x^{(i)} - \mu_x} {\sigma_x} \end{align}$$

其中，$x^{(i)}$ 和 $x_{std}^{(i)}$ 分别表示第 $i$ 个样本标准化前后的特征值，$\mu_x$ 和 $\sigma_x$ 分别表示该特征的平均值和标准差。

在 scikit-learn 中，可通过 sklearn.preprocessing.StandardScaler 实现：

>>> from sklearn.preprocessing import StandardScaler
>>> stdsc = StandardScaler()
>>> X_train_std = stdsc.fit_transform(X_train)
>>> X_test_std = stdsc.transform(X_test)